The Gent hyperelastic material model [ 1] rubber elasticity that is based on the concept of limiting chain extensibility. In this model, the strain energy density function is designed such that it has a singularity when the first invariant of the left Cauchy-Green deformation tensor reaches a limiting value
I
m
{\displaystyle I_{m}}
The strain energy density function for the Gent model is [ 1]
W
=
−
μ
J
m
2
ln
(
1
−
I
1
−
3
J
m
)
{\displaystyle W=-{\cfrac {\mu J_{m}}{2}}\ln \left(1-{\cfrac {I_{1}-3}{J_{m}}}\right)}
where
μ
{\displaystyle \mu }
shear modulus and
J
m
=
I
m
−
3
{\displaystyle J_{m}=I_{m}-3}
In the limit where
J
m
→
∞
{\displaystyle J_{m}\rightarrow \infty }
Neo-Hookean solid model. This can be seen by expressing the Gent model in the form
W
=
−
μ
2
x
ln
[
1
−
(
I
1
−
3
)
x
]
;
x
:=
1
J
m
{\displaystyle W=-{\cfrac {\mu }{2x}}\ln \left[1-(I_{1}-3)x\right]~;~~x:={\cfrac {1}{J_{m}}}}
A Taylor series expansion of
ln
[
1
−
(
I
1
−
3
)
x
]
{\displaystyle \ln \left[1-(I_{1}-3)x\right]}
x
=
0
{\displaystyle x=0}
x
→
0
{\displaystyle x\rightarrow 0}
W
=
μ
2
(
I
1
−
3
)
{\displaystyle W={\cfrac {\mu }{2}}(I_{1}-3)}
which is the expression for the strain energy density of a Neo-Hookean solid.
Several compressible versions of the Gent model have been designed. One such model has the form[ 2] [ 3]
W
=
−
μ
J
m
2
ln
(
1
−
I
1
−
3
J
m
)
+
κ
2
(
J
2
−
1
2
−
ln
J
)
4
{\displaystyle W=-{\cfrac {\mu J_{m}}{2}}\ln \left(1-{\cfrac {I_{1}-3}{J_{m}}}\right)+{\cfrac {\kappa }{2}}\left({\cfrac {J^{2}-1}{2}}-\ln J\right)^{4}}
where
J
=
det
(
F
)
{\displaystyle J=\det({\boldsymbol {F}})}
κ
{\displaystyle \kappa }
bulk modulus , and
F
{\displaystyle {\boldsymbol {F}}}
deformation gradient .
Consistency condition
We may alternatively express the Gent model in the form
W
=
C
0
ln
(
1
−
I
1
−
3
J
m
)
{\displaystyle W=C_{0}\ln \left(1-{\cfrac {I_{1}-3}{J_{m}}}\right)}
For the model to be consistent with linear elasticity , the following condition has to be satisfied:
2
∂
W
∂
I
1
(
3
)
=
μ
{\displaystyle 2{\cfrac {\partial W}{\partial I_{1}}}(3)=\mu }
where
μ
{\displaystyle \mu }
shear modulus of the material.
Now, at
I
1
=
3
(
λ
i
=
λ
j
=
1
)
{\displaystyle I_{1}=3(\lambda _{i}=\lambda _{j}=1)}
∂
W
∂
I
1
=
−
C
0
J
m
{\displaystyle {\cfrac {\partial W}{\partial I_{1}}}=-{\cfrac {C_{0}}{J_{m}}}}
Therefore, the consistency condition for the Gent model is
−
2
C
0
J
m
=
μ
⟹
C
0
=
−
μ
J
m
2
{\displaystyle -{\cfrac {2C_{0}}{J_{m}}}=\mu \,\qquad \implies \qquad C_{0}=-{\cfrac {\mu J_{m}}{2}}}
The Gent model assumes that
J
m
≫
1
{\displaystyle J_{m}\gg 1}
The Cauchy stress for the incompressible Gent model is given by
σ
=
−
p
I
+
2
∂
W
∂
I
1
B
=
−
p
I
+
μ
J
m
J
m
−
I
1
+
3
B
{\displaystyle {\boldsymbol {\sigma }}=-p~{\boldsymbol {\mathit {I}}}+2~{\cfrac {\partial W}{\partial I_{1}}}~{\boldsymbol {B}}=-p~{\boldsymbol {\mathit {I}}}+{\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}~{\boldsymbol {B}}}
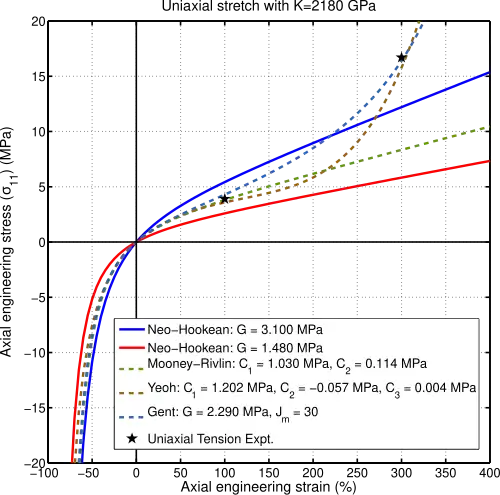
Uniaxial extension
Stress-strain curves under uniaxial extension for Gent model compared with various hyperelastic material models. For uniaxial extension in the
n
1
{\displaystyle \mathbf {n} _{1}}
principal stretches are
λ
1
=
λ
,
λ
2
=
λ
3
{\displaystyle \lambda _{1}=\lambda ,~\lambda _{2}=\lambda _{3}}
λ
1
λ
2
λ
3
=
1
{\displaystyle \lambda _{1}~\lambda _{2}~\lambda _{3}=1}
λ
2
2
=
λ
3
2
=
1
/
λ
{\displaystyle \lambda _{2}^{2}=\lambda _{3}^{2}=1/\lambda }
I
1
=
λ
1
2
+
λ
2
2
+
λ
3
2
=
λ
2
+
2
λ
.
{\displaystyle I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=\lambda ^{2}+{\cfrac {2}{\lambda }}~.}
The left Cauchy-Green deformation tensor can then be expressed as
B
=
λ
2
n
1
⊗
n
1
+
1
λ
(
n
2
⊗
n
2
+
n
3
⊗
n
3
)
.
{\displaystyle {\boldsymbol {B}}=\lambda ^{2}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\cfrac {1}{\lambda }}~(\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\mathbf {n} _{3}\otimes \mathbf {n} _{3})~.}
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have
σ
11
=
−
p
+
λ
2
μ
J
m
J
m
−
I
1
+
3
;
σ
22
=
−
p
+
μ
J
m
λ
(
J
m
−
I
1
+
3
)
=
σ
33
.
{\displaystyle \sigma _{11}=-p+{\cfrac {\lambda ^{2}\mu J_{m}}{J_{m}-I_{1}+3}}~;~~\sigma _{22}=-p+{\cfrac {\mu J_{m}}{\lambda (J_{m}-I_{1}+3)}}=\sigma _{33}~.}
If
σ
22
=
σ
33
=
0
{\displaystyle \sigma _{22}=\sigma _{33}=0}
p
=
μ
J
m
λ
(
J
m
−
I
1
+
3
)
.
{\displaystyle p={\cfrac {\mu J_{m}}{\lambda (J_{m}-I_{1}+3)}}~.}
Therefore,
σ
11
=
(
λ
2
−
1
λ
)
(
μ
J
m
J
m
−
I
1
+
3
)
.
{\displaystyle \sigma _{11}=\left(\lambda ^{2}-{\cfrac {1}{\lambda }}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~.}
The engineering strain is
λ
−
1
{\displaystyle \lambda -1\,}
engineering stress is
T
11
=
σ
11
/
λ
=
(
λ
−
1
λ
2
)
(
μ
J
m
J
m
−
I
1
+
3
)
.
{\displaystyle T_{11}=\sigma _{11}/\lambda =\left(\lambda -{\cfrac {1}{\lambda ^{2}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~.}
Equibiaxial extension
For equibiaxial extension in the
n
1
{\displaystyle \mathbf {n} _{1}}
n
2
{\displaystyle \mathbf {n} _{2}}
principal stretches are
λ
1
=
λ
2
=
λ
{\displaystyle \lambda _{1}=\lambda _{2}=\lambda \,}
λ
1
λ
2
λ
3
=
1
{\displaystyle \lambda _{1}~\lambda _{2}~\lambda _{3}=1}
λ
3
=
1
/
λ
2
{\displaystyle \lambda _{3}=1/\lambda ^{2}\,}
I
1
=
λ
1
2
+
λ
2
2
+
λ
3
2
=
2
λ
2
+
1
λ
4
.
{\displaystyle I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=2~\lambda ^{2}+{\cfrac {1}{\lambda ^{4}}}~.}
The left Cauchy-Green deformation tensor can then be expressed as
B
=
λ
2
n
1
⊗
n
1
+
λ
2
n
2
⊗
n
2
+
1
λ
4
n
3
⊗
n
3
.
{\displaystyle {\boldsymbol {B}}=\lambda ^{2}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda ^{2}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+{\cfrac {1}{\lambda ^{4}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}~.}
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have
σ
11
=
(
λ
2
−
1
λ
4
)
(
μ
J
m
J
m
−
I
1
+
3
)
=
σ
22
.
{\displaystyle \sigma _{11}=\left(\lambda ^{2}-{\cfrac {1}{\lambda ^{4}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)=\sigma _{22}~.}
The engineering strain is
λ
−
1
{\displaystyle \lambda -1\,}
engineering stress is
T
11
=
σ
11
λ
=
(
λ
−
1
λ
5
)
(
μ
J
m
J
m
−
I
1
+
3
)
=
T
22
.
{\displaystyle T_{11}={\cfrac {\sigma _{11}}{\lambda }}=\left(\lambda -{\cfrac {1}{\lambda ^{5}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)=T_{22}~.}
Planar extension
Planar extension tests are carried out on thin specimens which are constrained from deforming in one direction. For planar extension in the
n
1
{\displaystyle \mathbf {n} _{1}}
n
3
{\displaystyle \mathbf {n} _{3}}
principal stretches are
λ
1
=
λ
,
λ
3
=
1
{\displaystyle \lambda _{1}=\lambda ,~\lambda _{3}=1}
λ
1
λ
2
λ
3
=
1
{\displaystyle \lambda _{1}~\lambda _{2}~\lambda _{3}=1}
λ
2
=
1
/
λ
{\displaystyle \lambda _{2}=1/\lambda \,}
I
1
=
λ
1
2
+
λ
2
2
+
λ
3
2
=
λ
2
+
1
λ
2
+
1
.
{\displaystyle I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=\lambda ^{2}+{\cfrac {1}{\lambda ^{2}}}+1~.}
The left Cauchy-Green deformation tensor can then be expressed as
B
=
λ
2
n
1
⊗
n
1
+
1
λ
2
n
2
⊗
n
2
+
n
3
⊗
n
3
.
{\displaystyle {\boldsymbol {B}}=\lambda ^{2}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\cfrac {1}{\lambda ^{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\mathbf {n} _{3}\otimes \mathbf {n} _{3}~.}
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have
σ
11
=
(
λ
2
−
1
λ
2
)
(
μ
J
m
J
m
−
I
1
+
3
)
;
σ
22
=
0
;
σ
33
=
(
1
−
1
λ
2
)
(
μ
J
m
J
m
−
I
1
+
3
)
.
{\displaystyle \sigma _{11}=\left(\lambda ^{2}-{\cfrac {1}{\lambda ^{2}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~;~~\sigma _{22}=0~;~~\sigma _{33}=\left(1-{\cfrac {1}{\lambda ^{2}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~.}
The engineering strain is
λ
−
1
{\displaystyle \lambda -1\,}
engineering stress is
T
11
=
σ
11
λ
=
(
λ
−
1
λ
3
)
(
μ
J
m
J
m
−
I
1
+
3
)
.
{\displaystyle T_{11}={\cfrac {\sigma _{11}}{\lambda }}=\left(\lambda -{\cfrac {1}{\lambda ^{3}}}\right)\left({\cfrac {\mu J_{m}}{J_{m}-I_{1}+3}}\right)~.}
Simple shear
The deformation gradient for a simple shear deformation has the form[ 4]
F
=
1
+
γ
e
1
⊗
e
2
{\displaystyle {\boldsymbol {F}}={\boldsymbol {1}}+\gamma ~\mathbf {e} _{1}\otimes \mathbf {e} _{2}}
where
e
1
,
e
2
{\displaystyle \mathbf {e} _{1},\mathbf {e} _{2}}
γ
=
λ
−
1
λ
;
λ
1
=
λ
;
λ
2
=
1
λ
;
λ
3
=
1
{\displaystyle \gamma =\lambda -{\cfrac {1}{\lambda }}~;~~\lambda _{1}=\lambda ~;~~\lambda _{2}={\cfrac {1}{\lambda }}~;~~\lambda _{3}=1}
In matrix form, the deformation gradient and the left Cauchy-Green deformation tensor may then be expressed as
F
=
[
1
γ
0
0
1
0
0
0
1
]
;
B
=
F
⋅
F
T
=
[
1
+
γ
2
γ
0
γ
1
0
0
0
1
]
{\displaystyle {\boldsymbol {F}}={\begin{bmatrix}1&\gamma &0\\0&1&0\\0&0&1\end{bmatrix}}~;~~{\boldsymbol {B}}={\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}={\begin{bmatrix}1+\gamma ^{2}&\gamma &0\\\gamma &1&0\\0&0&1\end{bmatrix}}}
Therefore,
I
1
=
t
r
(
B
)
=
3
+
γ
2
{\displaystyle I_{1}=\mathrm {tr} ({\boldsymbol {B}})=3+\gamma ^{2}}
and the Cauchy stress is given by
σ
=
−
p
1
+
μ
J
m
J
m
−
γ
2
B
{\displaystyle {\boldsymbol {\sigma }}=-p~{\boldsymbol {\mathit {1}}}+{\cfrac {\mu J_{m}}{J_{m}-\gamma ^{2}}}~{\boldsymbol {B}}}
In matrix form,
σ
=
[
−
p
+
μ
J
m
(
1
+
γ
2
)
J
m
−
γ
2
μ
J
m
γ
J
m
−
γ
2
0
μ
J
m
γ
J
m
−
γ
2
−
p
+
μ
J
m
J
m
−
γ
2
0
0
0
−
p
+
μ
J
m
J
m
−
γ
2
]
{\displaystyle {\boldsymbol {\sigma }}={\begin{bmatrix}-p+{\cfrac {\mu J_{m}(1+\gamma ^{2})}{J_{m}-\gamma ^{2}}}&{\cfrac {\mu J_{m}\gamma }{J_{m}-\gamma ^{2}}}&0\\{\cfrac {\mu J_{m}\gamma }{J_{m}-\gamma ^{2}}}&-p+{\cfrac {\mu J_{m}}{J_{m}-\gamma ^{2}}}&0\\0&0&-p+{\cfrac {\mu J_{m}}{J_{m}-\gamma ^{2}}}\end{bmatrix}}}
References
^ a b Gent, A.N., 1996, A new constitutive relation for rubber , Rubber Chemistry Tech., 69, pp. 59-61.
^ Mac Donald, B. J., 2007, Practical stress analysis with finite elements , Glasnevin, Ireland.
^ Horgan, Cornelius O.; Saccomandi, Giuseppe (2004-11-01). "Constitutive Models for Compressible Nonlinearly Elastic Materials with Limiting Chain Extensibility" Journal of Elasticity . 77 (2): 123– 138. doi :10.1007/s10659-005-4408-x . ISSN 1573-2681 . ^ Ogden, R. W., 1984, Non-linear elastic deformations , Dover.
See also