Snub dodecadodecahedron

Snub dodecadodecahedron
Type	Uniform star polyhedron
Elements	F = 84, E = 150 V = 60 (χ = −6)
Faces by sides	60{3}+12{5}+12{5/2}
Coxeter diagram
Wythoff symbol	| 2 5/2 5
Symmetry group	I, [5,3]+, 532
Index references	U40, C49, W111
Dual polyhedron	Medial pentagonal hexecontahedron
Vertex figure	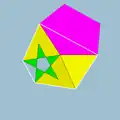3.3.5/2.3.5
Bowers acronym	Siddid

In geometry, the snub dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U₄₀. It has 84 faces (60 triangles, 12 pentagons, and 12 pentagrams), 150 edges, and 60 vertices.^[1] It is given a Schläfli symbol sr{5⁄2,5}, as a snub great dodecahedron.

Let ${\displaystyle \xi \approx 1.2223809502469911}$ be the smallest real zero of the polynomial ${\displaystyle P=2x^{4}-5x^{3}+3x+1}$. Denote by ${\displaystyle \phi }$ the golden ratio. Let the point ${\displaystyle p}$ be given by

${\displaystyle p={\begin{pmatrix}\phi ^{-2}\xi ^{2}-\phi ^{-2}\xi +\phi ^{-1}\\-\phi ^{2}\xi ^{2}+\phi ^{2}\xi +\phi \\\xi ^{2}+\xi \end{pmatrix}}}$.

Let the matrix ${\displaystyle M}$ be given by

${\displaystyle M={\begin{pmatrix}1/2&-\phi /2&1/(2\phi )\\\phi /2&1/(2\phi )&-1/2\\1/(2\phi )&1/2&\phi /2\end{pmatrix}}}$.

${\displaystyle M}$ is the rotation around the axis ${\displaystyle (1,0,\phi )}$ by an angle of ${\displaystyle 2\pi /5}$, counterclockwise. Let the linear transformations ${\displaystyle T_{0},\ldots ,T_{11}}$ be the transformations which send a point ${\displaystyle (x,y,z)}$ to the even permutations of ${\displaystyle (\pm x,\pm y,\pm z)}$ with an even number of minus signs. The transformations ${\displaystyle T_{i}}$ constitute the group of rotational symmetries of a regular tetrahedron. The transformations ${\displaystyle T_{i}M^{j}}$ ${\displaystyle (i=0,\ldots ,11}$, ${\displaystyle j=0,\ldots ,4)}$ constitute the group of rotational symmetries of a regular icosahedron. Then the 60 points ${\displaystyle T_{i}M^{j}p}$ are the vertices of a snub dodecadodecahedron. The edge length equals ${\displaystyle 2(\xi +1){\sqrt {\xi ^{2}-\xi }}}$, the circumradius equals ${\displaystyle (\xi +1){\sqrt {2\xi ^{2}-\xi }}}$, and the midradius equals ${\displaystyle \xi ^{2}+\xi }$.

For a great snub icosidodecahedron whose edge length is 1, the circumradius is

${\displaystyle R={\frac {1}{2}}{\sqrt {\frac {2\xi -1}{\xi -1}}}\approx 1.2744398820380232}$

Its midradius is

${\displaystyle r={\frac {1}{2}}{\sqrt {\frac {\xi }{\xi -1}}}\approx 1.1722614951149297}$

The other real root of P plays a similar role in the description of the Inverted snub dodecadodecahedron

Medial pentagonal hexecontahedron
Type	Star polyhedron
Face
Elements	F = 60, E = 150 V = 84 (χ = −6)
Symmetry group	I, [5,3]+, 532
Index references	DU40
dual polyhedron

The medial pentagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the snub dodecadodecahedron. It has 60 intersecting irregular pentagonal faces.

• List of uniform polyhedra
• Inverted snub dodecadodecahedron

• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208

• Weisstein, Eric W. "Medial pentagonal hexecontahedron". MathWorld.
• Weisstein, Eric W. "Snub dodecadodecahedron". MathWorld.