Sphere packing in a sphere

Sphere packing in a sphere is a three-dimensional packing problem with the objective of packing a given number of equal spheres inside a unit sphere. It is the three-dimensional equivalent of the circle packing in a circle problem in two dimensions.

Number of inner spheres	Maximum radius of inner spheres[1]		Packing density[2]	Optimality	Arrangement	Diagram
	Exact form	Approximate
1	${\displaystyle 1}$	1.0000	1	Trivially optimal.	Point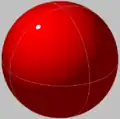
2	${\displaystyle {\dfrac {1}{2}}}$	0.5000	0.25	Trivially optimal.	Line segment
3	${\displaystyle 2{\sqrt {3}}-3}$	0.4641...	0.29988...	Trivially optimal.	Triangle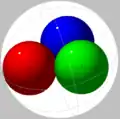
4	${\displaystyle {\sqrt {6}}-2}$	0.4494...	0.36326...	Proven optimal.	Tetrahedron
5	${\displaystyle {\sqrt {2}}-1}$	0.4142...	0.35533...	Proven optimal.	Trigonal bipyramid
6	${\displaystyle {\sqrt {2}}-1}$	0.4142...	0.42640...	Proven optimal.	Octahedron
7	${\displaystyle {\frac {1}{{\frac {{\sqrt {3}}+2\cos \left({\frac {\pi }{18}}\right)}{\sqrt {2+2{\sqrt {3}}\cos \left({\frac {\pi }{18}}\right)}}}+1}}}$	0.3859...	0.40231...	Proven optimal.	Capped octahedron
8	${\displaystyle {\frac {1}{{\sqrt {2+{\frac {1}{\sqrt {2}}}}}+1}}}$	0.3780...	0.43217...	Proven optimal.	Square antiprism
9	${\displaystyle {\frac {{\sqrt {3}}-1}{2}}}$	0.3660...	0.44134...	Proven optimal.	Tricapped trigonal prism
10		0.3530...	0.44005...	Proven optimal.
11	${\displaystyle {\dfrac {{\sqrt {5}}-3}{2}}+{\sqrt {5-2{\sqrt {5}}}}}$	0.3445...	0.45003...	Proven optimal.	Diminished icosahedron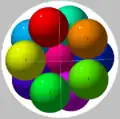
12	${\displaystyle {\dfrac {{\sqrt {5}}-3}{2}}+{\sqrt {5-2{\sqrt {5}}}}}$	0.3445...	0.49095...	Proven optimal.	Icosahedron